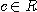)とする。 大石 進一 日本シミュレーション学会誌Vol. 19 No.3 (2000年9月号) よりHTMLに変換転載
このページのURIは http://www.oishi.info.waseda.ac.jp/~oishi/LINKS/kai2.htm
本稿では精度保証付き数値計算を行うための環境を整備するためのweb情報を詳細に記述する。また、 線形連立方程式の数値解の精度保証が、ガウスの消去法による数値解を求めるのと同じ手間で可能となることを示す。 この結果、線形系については精度保証付き数値計算がほぼ実用段階に到達したことを明らかにする。
In this article, it is shown how to build computational environment to perform numerical simulation with guaranteed accuracy. For the purpose, detailed web information is cited. It is also shown that verification of numerical solution of the simultaneous linear equation can be performed with the computational $n^3/3$ flops which is same as that for calculating a numerical solution of the problem by the Gauss elimination.
結果の精度が保証された数値計算を精度保証付き数値計算という。区間演算や丸め制御による数値計算によって、精度保証付き 数値計算が可能であることが示されている。本学会誌でも講座として精度保証付きシミュレーション\cite{K1}$\sim$\cite{K4}が 連載され、その全体像が把握できるので参照されたい。また、精度保証付き数値計算の専門書が 出版され、深くこの分野が学べるようにもなりつつある。数値計算とは精度保証付き数値計算であるという立場からの 数値計算の入門書も出版されている。 一方、現在普通に行われている数値計算は結果の精度を保証することは考えられていない。 これを近似計算と呼ぶことにしよう。近似計算の結果を基にして、近似解の近くに真の解が存在し、その真の解と近似解の 誤差を精度保証付き数値計算で計算することを、数値計算結果の検証(verification)と呼ぶ。また、近似解を得た後で、 その誤差を計算するので、数値計算結果の検証は事後誤差解析(a posteriori error estimate)の一種となる。 一方、あまり規模の大きい計算には向かないが、近似解を求めることなく、すべての計算を精度保証付きで進めることに よって、問題を解く方法も考えられている。 精度保証付き数値計算という言葉は、事後誤差解析的に真の解の存在を示し、更に近似解の誤差を計算する場合も、すべての計算を 精度保証付きで進めることによって、問題を解く場合も含めて指すことが多い。本稿では、文献\cite{K1}$\sim$\cite{O1} を補足して、精度保証付き数値計算を行うための計算機環境を整えるためのweb情報や、連立一次方程式の精度保証が、 数値解をもう一回求める手間で行えるなどの精度保証付き数値計算の研究の 最近の話題につき解説することを目的としている。特に、つぎの点について重点的に解説する。
以上を要するに、現代の研究においては、webの利用が不可欠になっている。この点を重視した精度保証付き数値計算の解説になること を目指して本稿は執筆されている。 \section{数値計算ツール} 精度保証付き数値計算はやはり数値計算である。したがって、まず、数値計算のツールとしてどのようなものがあるかを知ること が重要となる。まず、数値計算に関連するサイトを紹介しよう。よくある質問とその解答のサイトとして
FAQ Numerical Analysis and Associated Fields Resource Guide
がある。この中には数値計算パッケージや数値計算ソフトウエアへのリンクもあり、基本的な数値計算ツールを揃えるのに便利である。 また、最適化に関連する数値計算のサイトとしては
Bibliography for Optimization with Sensitivity Analysis
がある。
まず、線形計算のためのツールとして、メモリ階層(キャッシュヒット率)を考えた、 信頼性のあるパッケージとしてLAPACK(レイパックと発音する)がある。 これは、Oak Ridge National Laboratory,Knoxville, TennesseeとAT\&T Bell Laboratories, Murray Hill, NJに置かれている
からダウンロードできる。日本のミラーサイトとしては
がある。
LAPACKのユーザマニュアル第3版がある。第2版は日本語訳がある。LAPACKはもともとFORTRANで書かれているライブラリであるが、 CLAPACKはそのC版である。LAPACKはCPUによる違いをBLAS(Basic Linear ALgebraic Library)によって吸収してある。すなわち、 線形代数の基本演算をBLASの関数にし、これを標準化している。そして、LAPACK本体をBLASを用いて書くことによってポータブル化を 図っている。自分の使用するCPUに対して最適化されているBLAS(アセンブラ)を用いることによって、Cで書かれたBLASを 用いた場合の数十倍の高速化が達成されている。線形方程式の直接解法に関しては、最適化BLASとLAPACKの組み合わせは、最も 優れた組み合わせの一つとなる。
がある。 現在はまだPentium III用のBLASは開発されていないようである。Cのコンパイラの 特性を考えてループ展開などの技法を駆使して、Cで書かれているにもかかわらず、コンパイル時にループ展開の数などのパラメータを 最適化することによって最適化BLASに匹敵するオブジェクトコードを生成する試みもある。
である。尚、PHIPACKは dgemmという行列の乗算プログラムだけが対象にされている。原理的には、どのようなCPUとOSであっても、Cコンパイラがあれば、 CでかかれたATLASやPHIPACKをコンパイルするだけで最適化BLASに匹敵するコードが得られる。線形代数計算の直接解法に関しては 最も高速で、信頼性を求めるならLAPACKと最適化BLASを実装するのが有力な解となる。 LAPACK++はC++ versionであるが、LAPACKの一部の関数しか実装されていない。また、分散マシン上のLAPACKとして ScaLAPACKが開発されている。数値計算パッケージの紹介としてはつぎのようなサイトもある
1.数値計算のコードを載せた本として、しばしば利用される向きのあるNumerical Recipesは数値計算の専門家でない著者による 書であるが、つぎのような批判
がある。これらの批判はこの本に載せてあるコードが最適なものに比べて実行速度が数十倍遅く、 また、信頼性も低い場合があるという点に集中している。 Netlibなどの他の優良なソフトを利用すべきであろう。
2.本稿では反復解法は扱わないが、 数値線形代数の反復解法のサーベイがある。
LAPACKなどの数値計算ライブラリは高速、高信頼であるが、CやFORTRANから呼び出して使うの、 プログラム開発に時間がかかる。 そこで、LAPACKなどのライブラリを基礎にして、使い易いGUIをもたせた数値計算用インタプリタパッケージが開発されている。 The MathWorks, Inc.から発売されている
はその代表である。 欧米では、研究者から、学生までこのようなパッケージを利用して数値計算をするのが 一般的である。
MATCOM(Matlab to C++ Compiler)
はMatlabからC++へのコンパイラ、 すなわちMatlabコードからMEXファイルあるいはC++コードを生成するフリーなツールである。 生成されたC++コードを最適化されたC++コンパイラでコンパイルするとMatlabより数段高速なコードとなる。
MAT
W. KahanによるMatlab's Loss is Nobody's Gainは Matlabに対する面白いコメントである。 また、つぎのようなフリーなパッケージソフトがある。
1.Octaveは MATLABに最も近いMATLABクローンである。Linux用のソフトであるが、
こともできる。 まだ、オブジェクトプログラミングが実装されていない点ではMATLABに譲るが、 線型方程式の解や固有値を計算する組み込み関数の計算速度、信頼性ではMATLABに勝るとも劣らないと思われれる。 グラフィックスはgnuplotを利用している。また、
ATLASを使ってOctaveを高速化することもできる (Tuning up Octave by ATLAS)。
ATLASによる高速化の効果は大変大きく、Alpha/EV56/533MHzで、2つの$1000 \times 1000$行列の積の計算に reference BLAS(Cで書かれた高速化していないBLAS)とOctaveの組み合わせでは54.7秒かかっていたものが、 ATLASを使うと4.0秒で計算できるようになったとの報告が書かれている。
2.Scilabは typed listによりオブジェクト指向プログラミングができる環境があり、MATLABクローンとしては一番完成している。 グラフィックスも独自の優れたものが実装されている。MAPLEとのリンクもできる。LinuxでもWindowsでも実装できる。
3.Telaは大規模数値計算のプロトタイピング言語となることを目指して作られており、 グラフィックス、線形代数、FFTなどを 装備して偏微分方程式を解くことを念頭にしている。
4.RLaBは行列数学用パッケージ。
5.Eulerは実数、複素数、区間などを扱えるMatlabクローンな言語。 Linux版はフリーで、Windows版はシェアウエアである。
6.Prophet}はUnix上のライフサイエンス用言語。
7.Yorickは型チェックをしないCライクなLinux上の数値計算 インタプリタ言語。 SpYorick}はYorickのプラグインで疎行列処理をする。
8.PETScはMPIを用いた偏微分方程式の並列数値計算用のツール。unix上の CやC++から呼び出して使う。
9.Ascendはフリーな強い型付けされたオブジェクト指向モデル記述言語。
10. Algae}(Alkiが前身)は疎系に対してMatlabより高速であることを ねらったMatlabクローン的なインタプリタ数値計算言語。
著者は、MatlabとOctaveとScilabを利用している。Matlab互換のScilabによる線形連立方程式の解法の例を次に示す。
-->A=[1 2;2 1]
A = ! 1. 2. !
! 2. 1. !
-->b=[1;1]
b = ! 1. !
! 1. !
-->x=A\b
x = ! 0.3333333 !
! 0.3333333 !
-->A*x-b
ans = ! 0. !
! 0. !
このように非常に簡単に(かつ高速に)線形方程式が解ける。詳細は著者によるMatalab, Octave, Scilabの使い方などを参照されたい(そのテキスト(拙著「Linux数値計算ツール(コロナ社)」)も出版された)。 Demmelの著書\cite{D}のMatlabコードがあるのでよいプログラム例として参考にされたい。
精度保証付き数値計算の基礎は、コンピュータ上での四則演算である。高速なハードウエアでの演算が実現されている 浮動小数点演算とソフト的に演算を実行する多倍長演算に分けて議論しよう。 \subsection{浮動小数点演算} 現在の浮動小数点演算はIEEE754規格に基ずくものが標準的である。これは優れた数値計算学者であるKahanらの努力により1985年に 制定された。その内容については、当事者である
を読むのがよいであろう。制定の歴史を語った文書もある
(An Interview with the Old Man of Floating-Point)。
現在ではIntelのPentium CPUを含むほとんどのマシンがIEEE754に従っているが、どのようなCPUが例外かなどは
Interval FAQの記録:What machines support IEEE754?
が参考になる。また、IEEE754にしたがってどのように浮動小数点演算が実装されているかの例は、例えば、
IntelのPentiumIIIのマニュアルなどを見るとよい。 与えれたCPUがIEEE754規格を満たしているかどうかをチェックするプログラムが存在する
(TestFloat)。
TestFloat1はソフトウエアでシミュレートされた浮動小数点システム
と対象としているハードウエアの実行結果を比較して、違いが あるとバグの候補として出力するようなソフトウエアである。
IEEE754によって標準化されているのは2進の倍精度浮動小数点数である。浮動小数点数を利用した精度保証付き計算には IEEE754の丸め(以下に示すものの中で上と下への丸め)を利用する。cを実数(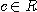)とする。
これ以外にも近似計算のデフォールトの丸めである最近点への丸め(round to nearest)と チョッピング(切り捨て)(round toward 0)の丸めがある。
IEEE754では浮動小数点数演算($\F$上での四則演算) は丸めとの関係によりつぎのように定義されている。 ・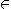
{+,-,×,/} ，○ 
{△,▽}
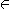のとき
x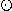 
y = ○(x ・y) (任意の
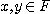について)}
この式は，左辺の浮動小数点数の四則演算の結果x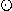 
yは， 右辺の数学的に正しい(実数としての)四則演算の 結果x ・yを指定された丸めを行って得られた数○
(x ・y) に一致するように計算する規格を表している。 また，平方根も
= ○(
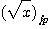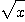) (任意の
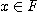について)
と，浮動小数点数演算によって計算された平方根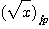
は，正確な 実数演算で計算された平方根
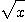を指定された丸めの方向へ丸めた数となる
規格である。
注意すべきことは，指数関数や三角関数などはこのような規格を みたすようには規定されていないことである。 この事に関しては初等関数などの実装の研究者J.-M. Mullerの
The Table Maker's Dilemma:our search for worst cases
が参考になる。 定理証明システム(HOL Light)を使って、指数関数などのマシンへの実装がIEEE754にしたがっているかどうかを チェックするような試みもある
(Floating Point Verification)。
このように、初等関数の値を 精度保証付きで求めるためには別途工夫が必要である。
浮動小数点数は実数の近似であるので、一つの浮動小数点数だけでは、誤差を表現することができない。そこで、 求めたい実数の下界と上界を表す2つの浮動小数点数のペアで誤差まで表現することが考えられた。すなわち、 実数を両端を浮動小数点数とする区間で表すという考え方である。このような考え方の芽は数学においては 1900年代の半ばころには存在していたが、具体的に区間を基礎データ型とする数値計算を唱えたのは
である。これを区間解析という。現代の精度保証付き数値計算はすべて区間解析をベースとすると考えてよい。その 意味で精度保証付き数値計算の発祥地は日本である。これは1960年代のことであるが、区間解析が実用に近づくのは 非常に最近であるので、数値計算技術としては40年近くの紆余曲折がある。これは、区間解析の 基本演算である区間演算が単純でない性質をもっているからであり、これを基に効率的な精度保証数値計算を実行するのは 難しいからであった。すなわち、前章までに紹介した、プロの設計した数値計算ライブリや数値計算言語の高速性と信頼性を保ちながら 精度保証付き数値計算を実行する方法が見え出すまでに長い年月がかかったのである。本章では、区間解析の入門から 最新の状況までを眺めてみよう。
区間解析の情報を集めたサイトは区間解析の勉強に便利である。しかし、このサイトの区間解析の入門記事には須永の名前がなくMooreが区間解析のアイディアを 出したと勘違いしてる。須永の業績は国際的に引用されることも多いが、まだ十分ではない。このサイトの中で インターバル計算用の数値計算ライブラリやパッケージが紹介されているが、お勧めは
S.RumpのMatlabのツールボックスINTLAB
である。 丸めの制御、区間演算、自動スロープ計算(微係数の近似)、線形方程式の精度保証、精度保証された初等関数と区間への拡張、非線形方程式の精度保証などがユーザフレンドリに 実用的な速度で実行できる。数学的に精度の保証された初等関数を実用的にどのように実装するかのもでるとしてもC++の区間演算のクラスライブラリとして
がよい。
さて、区間演算の難しい点について述べよう。以下、区間はIEEE754に従う倍精度浮動小数点数を両端とする区間とする。 区間演算は区間を基本的なデータ型として、その四則演算のことである。2つの区間[a,b], [c,d]に対して 例えば区間演算の和は
down;
d=a+c;
up;
u=b+d;
と定義される。減算、乗除算も同様である。 区間演算をいちいち浮動小数点演算と区別して書くのは大変なので、通常演算子多重定義によって区間型を 定義して利用することが多い。ここで問題となるのは、既存の高速なパッケージでは四則演算の多重定義に対応していないことである。 また、丸めの向きの変更の命令down;,up;などの使用も考えていないことである。よって、現在の所、区間型を定義して 演算子多重定義により区間演算を実行すると、つぎのような不利益が考えられる。
これらの効果により、通常の数値計算に対して、その近似解の精度を検証しようとすると、簡単に100倍程度の計算時間がかかるのが 常であった。また、浮動小数点演算を区間演算に置き換えただけでは、区間幅が増大してしまい、 ゼロを含む区間による除算などが発生して、最後まで計算が 進まないことも経験された。これに対処するための様々な技法が開発され 単純な区間解析から現代の区間解析に変遷してきているというのが実情である。区間幅の拡大を防ぐために、自動微分の 考え方や
の考え方などが発生した。 これらによって、区間幅の増大はある程度制御できるようになったが、 実行速度の向上は望めなかった。これらは非線形系への適用に関する話題であるが、つい最近になって、線形系に 対しては、非常に効果のある高速化の手法が提案された。以下、章を改めてその話題を論じる。
著者はドイツの研究者Rumpとの共同研究で、丸めの制御計算による精度保証法を開発し、 線形連立方程式の数値解の精度保証が、数値解を求めるのと同じ計算量で理論的にも、実際計算(この場合には計算時間が
同程度となるという意味)でも実行できることを示した\cite{SO}。人間の計算でも、答えの検算は、もう一度やり直すのが 普通であるから、数値解を求めるのと同じ計算時間で、近似解と真の解の誤差がシャープに求まるというのは
理論的にもこれ以上高速化が望めないのではないかと推察される(Demmelのプレプリントによれば、厳密に条件数を計算する 計算量の下限はO(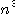
)flopsになることが示される)。
丸めの制御計算による精度保証 方式とは、区間演算を演算子多重定義することなしに実装することを考えて考案されたもので、線形演算に区間演算を 制御する場合に適用できる。
基礎は内積計算である。n次元ベクトルu=(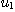
,
,・・・,
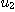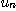)'とv=(
,
,・・・,
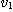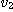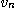)'を考える。ただし、 
,
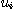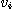はi=1,2,・・・,nに対して倍精度浮動小数点数であるとする。このとき、uとvの内積zを計算すること
を考えよう。よく考えると
down;
zd=u'*v;
up;
zu=u'*v;
とするとz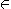 
[z_d,z_u]となることがわかる。ただし、以上の計算はMatlab的に計算したものとする。Matlabでは ベクトルu,vに対してu'*vはベクトルの内積として演算子多重定義されており、内部では
LAPACK(場合によりLINPACK)のベクトルの和のライブラリ関数が呼び出されて計算 される。もちろん、最高に高速化を望む場合は、CやFORTLANでプログラムを書いてLAPACKと速いBLASの組み合わせで、
LAPACKの和の計算関数を呼び出して計算する。丸めの制御計算方式とは、従来の高速パッケージ関数の関数を呼び出して 精度保証計算を進める方式で、従来の高速パッケージでは使用されていなかった丸めの制御命令が、関数呼び出しの
前と後に位置し、パーケージの呼び出し(ひいては高速化)の妨げにならないような計算方式のことを指すことにした。 以上の内積の精度保証計算が、通常の近似内積計算の2倍の計算速度で実行できることはプログラムを見てすぐにわかる。
内積計算が高速に精度保証できると、いわゆる数値線形代数のアルゴリズムは高速に精度保証することができる。 例えばAをn × n行列、bをnベクトルとすると、Ax=bの数値解の精度保証は基本的に内積計算の精度保証
方式を応用して実行できる。しかし、単純のプログラムを作成すると精度保証に数値解を得る計算時間の9倍の手間が かかる。これを、後退誤差解析の最新の成果を利用して、改良すると、精度保証の計算時間を1/9倍にできることを
著者はRumpとの共同研究で示した。すなわち、精度保証に要する計算時間が数値解を計算する手間と同じであることが示された。 以下、少し詳細にこの結果を紹介しよう。
連立一次方程式
Ax=b, (1)
を考える。ただし、 Aはn ×n実行列でxとbはn次元ベクトルとする。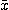 
を上式の数値解とする。このとき、つぎの定理はよく知られている。
定理 1 RをAの逆行列の近似とする。もし、
||
||
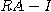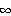
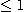
が成立するなら、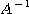
が存在して、次の評価が成立する:
||
||
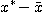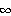<=(||R(A
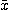-b)||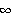
/(1-||RA-I||
),
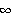ただし、$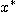
$は(1)の真の解とする。
RA-Iと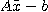
の包み込みを計算するプログラムは次のようになる。
down();
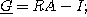
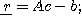
up();
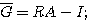
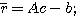
このプログラムを実行する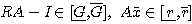
となる。これから||
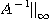と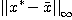
の上界を計算するプログラムは次のようになる。
}
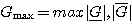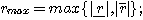
up();
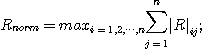
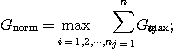
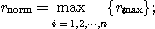
down();
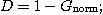
if(D > 0)
up();
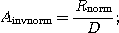
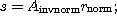
else
print("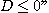
)};
このプログラムを実行したとき、D>0であれば、定理 1より
||x^*-c||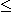 
s.
となることがわかる。cは数値解である。 このプログラムの計算量を評価してみる。逆行列Rの数値計算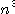
flopsかかり、RA-I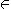 
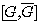という包み込みの計算に2
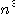flopsかかるので、総合して3
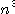flopsの計算量がかかることがわかる。これは、ガウス消去による数値解の計算量
$n^3/3$の9倍の手間である。数値解を得る手間の9倍で精度保証できることは、従来100倍ぐらいはかかっていたことに 比べれば、高速化されたことになるが、まだまだ精度保証のコストが高いといえる。
そこで、精度保証の高速化を図ることを考えよう。 そこで、次のような方針を取ることとする。 逆行列Rを計算する代わりに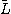
と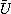
}の逆行列X_LとX_Uを計算する。
ただし、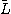
と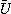
はガウス消去によってAを LU分解して得られたLとUとする。そして、Rの代わりにX_U ・X_Lを用いる。ただし、行列の積は計算しないものとする。
X_L計算量は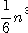
flopsでX_Uの計算量も
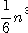flopsとなる。以下、これ以外の精度保証の 計算にはO
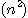の計算量の
計算しか現れないことを示そう。 定理 1 から
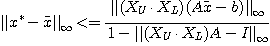
が成り立つ。ここで、 ||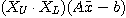
||という項は行列とベクトルの積となるのでO(
) flopsで計算できる。
高速化の 基本的なアイディアは次である。 L, U, 
及び
をガウスの消去アルゴリズムで最近点への丸めのモードで計算したとする。このとき、
最近得られたHighamによるWilkinson型の後退誤差解析を使うと
.
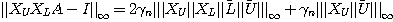という評価が得られることが示せる。これを使うと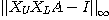
の評価が$O(
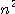)$ flopsで計算できる。 この公式を導くためには次のHighamによる補題が必要となる。
尚、Highamの著書\cite{H}の追加の情報やその
1000に及ぶ文献表を切り出したdviファイルもこの webサイトにある。
補題 1(Higham) 最近点への丸めのモードの下で、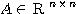
に対してガウスの消去法でLU分解
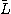と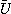
を計算したとする。このとき、
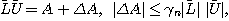
が成立する。ただし、
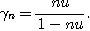
ここに、uは単位の丸めでIEEE 754の倍精度浮動少雨数点数に対しては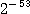
で与えられる。
補題 2 Tを三角正方行列とする。Tの左逆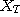
をガウスの消去法で計算したとする。このとき、
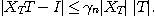
が成立する。
この二つの補題を使うと、
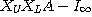
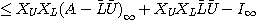
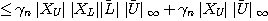
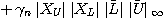
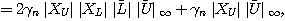
と所望の公式が導出できる。ここで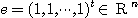
とすると 明らかに
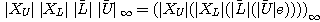
及び
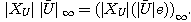
が成立する。 これは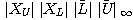 
と 
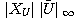が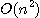
で計算できることを示している。 こうして、
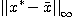が
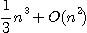flopsで計算できることがわかった。 例を示そう。上述の方法により，近似解とその精度保証をするC言語プログラムを 作りその計算時間を 測定した。実行時間の測定
結果をまとめて表\ref{t3-2}に示す。また，参考のために，IntelのPentium用に最適 化された BLASを用いたLAPACKを利用して作成したプログラムによる，
同じパソコン(Intel PentiumIII 600MHz)での計算時間も示す。
表1. LU分解を利用した近似解とその高速精度保証のための計算時間(sec)
|
n |
C |
MATLAB |
LAPACK（最適化BLAS) |
|
100 |
0 |
0.04 |
0.02 |
|
200 |
0.3 |
0.18 |
0.05 |
|
300 |
0.7 |
0.62 |
0.14 |
|
400 |
2 |
1.3 |
0.24 |
|
500 |
4 |
2.7 |
0.47 |
|
600 |
8 |
5 |
0.7 |
|
700 |
13 |
8 |
1.1 |
|
800 |
19 |
12 |
1.5 |
|
900 |
24 |
19 |
2.1 |
|
1000 |
37 |
24 |
2.8 |
固有値や得意の数値計算の精度保証の方式も丸めの制御方式で高速に実行できることも著者は示している\cite{SO2}。 こうして、数値線形代数に現れる問題の精度保証は、丸めの制御方式による精度保証で高速に実行できることが 明らかになってきた。実装についても、ユーザの 数値計算を普段実行してる環境の中で、精度保証付き数値計算が実行できることように考えられた方式なので、 実用性も高いと考えられる。 \section{今後の方向} 精度保証付き数値計算は、数値線形代数を皮切りに実用化され始めた。その実用化の方向が着実に進むためには 基本的な問題から解決しなければいけない問題も多い。以下に、そのような問題について議論しよう。
区間演算自身をより高速に実行できる環境を作るアプローチがある。区間演算をFORTRANなどの基本演算として 採用するように働きかける努力の結果、
は区間計算用に設計された}ことは既に述べた 。更に、プロポーザルの段階であるが、
開発の提案がある。
この内容はすでに別の資料にまとめてあるので、それを参照されたい。
\bibitem{K1} 柏木雅英: ``精度保証付き数値計算[1]--区間解析'',シミュレーション{\bf 18} 4, 261/267 (1999)
\bibitem{K2} 大石進一: ``精度保証付き数値計算[2]--線形方程式の高速精度保証とプログラミング技法'',シミュレーション{\bf 19} 1, 39/45 (2000)
\bibitem{K3} 神澤雄智、相馬隆郎: ``精度保証付き数値計算[3]--常微分方程式の精度保証'',シミュレーション{\bf 19} 2, 30/35 (2000)
\bibitem{K4} 中尾充宏: ``精度保証付き数値計算[4]--偏微分方程式の精度保証'',シミュレーション{\bf 19} 3 (2000)
\bibitem{O0} 大石進一: 非線形解析入門、コロナ社(2000)
\bibitem{NY} 中尾充宏、山本野人: 精度保証付き数値計算、日本評論社(1998)
\bibitem{O} 大石進一: 精度保証付き数値計算、コロナ社(2000) \bibitem{O1}大石進一: 数値計算、裳華房(1999)
\bibitem{OLinux} 大石進一: ``Linux数値計算ツール'',コロナ社(2000.9) \bibitem{D}J. Demmel: ``Applied Numerical Linear Algebra'', SIAM (1997)
\bibitem{SO} Shin'ichi Oishi and Siegfried M. Rump: ``Fast verification of solutions of matrix equations'', submitted to {\it Numer. Math.}.
\bibitem{H} Nicholas J. Higham: ``Accuracy and Stability of Numerical Algorithms'', SIAM (1996).
\bibitem{SO2}Shin'ichi OISHI: ``Fast Enclosure of Matrix Eigenvalues and Singular Values via Rounding Mode Controlled Computation'', to appear in {\it Linear Algebra and its Applications}
