第３章　回路の定常状態と過渡現象

本章のねらい（次を理解することを目標とする）

定数係数の線形常微分方程式の一般解は右辺を０（電源なし）と置いた斉次方程式の一般解と一つの特解の和で表わされること．
上記において右辺を定数（直流電源の値）と置いた特解は直流解であること．
上記の常微分方程式の右辺が正弦波である場合，同じ角周波数の正弦波に限定すれば，解（振幅と位相）は一意に定まる．これ（一つの特解）が正弦波交流を印加したときの定常解となること．この時点ではフェーザ法（複素表示）を導入していないので，計算は面倒になるが，三角関数の公式だけを用いて解析することになる．
微分方程式が１階(RL回路又はRC回路）である場合，変数分離形となるので簡単に一般解が求められる．ここで初期条件（t=0のときの変数値）を与えて任意定数を定めることによって得られた特解が回路の過渡現象（定常項と過渡項の和）であること．ラプラス変換を知らなくても，RL又はRC1次回路に直流又は正弦波交流を印加したときの過渡現象が求められる．

(1) 常微分方程式の基礎

回路方程式は一般には常微分方程式となる。集中定数回路の回路方程式は、定数係数の常微分方程式となる。とくに、線形な素子のみを考えているときには定数係数の線形常微分方程式となる。これは常微分方程式の中でももっとも易しいところで、解析も深く進んでいる。まず、定数係数の線形常微分方程式の理論を勉強しよう。それには

１階と２階の定数係数の線形常微分方程式（pdf）

が参考になる。ただし、これは英語である。しかし、大変易しい英語であるから、技術英語に慣れる意味で是非読んでみてほしい。

3.1　コンデンサの充放電

図のRC回路を考える。

スイッチをt=0で1から２へ入れたときの振る舞いを調べよう(コンデンサの充電)

　図3-1 RC直列回路

ただし、v(0)=0とする。

　図3-1の回路は図3-2の回路に書き直すことができる。ただし、u(t)はヘビサイドの単位ステップ関数とする。

　図3-2 図3-1と同等な回路

ただし、ヘビサイドの単位ステップ関数とは

　(3-1)

で与えられる関数である。図3-2の回路において、抵抗の両端の電圧をv1(t)とすると

v1(t)+v(t)=Vu(t) (3-2)

が成り立つ。v1(t)=Ri(t)でi(t)=Cdv/dtであるから式(3-2)は

(3-3)

となる。

一階の方程式の解

(3-3)を解くために、一階の線形な非斉次の定数係数常微分方程式の一般形

　(3-4)

を考える。

(a) 斉次方程式の一般解

　まず、(3-4)の右辺のf(t)をゼロとした斉次方程式を考える。

　(3-5)

この方程式(3-5)の解は

(3-6)

で与えられる。ただし、Aは定数である。この定数は初期条件(t=0でのxの値）から決めることができる。

(b) 非斉次方程式の一般解

非斉次方程式(3-4)の一般解は

　　　非斉次方程式(3-4)の一般解　＝　斉次方程式(3-5)の一般解　＋　非斉次方程式(3-4)の一つの解（特解）

という形をしている。非斉次方程式(3-4)の一つの解（特解）は

　(3-7)

である。よって、式(3-4)の一般解は

　(3-8)

で与えられる。

斉次方程式(3-5)の一般解は斉次であるように、電源によらない。また、Aという定数は初期値によって決めるので、初期値に依存する。これは、回路にスイッチが入ったときに、初期条件から定常状態に移行する過程に現れるもの（過渡状態を表す解）である。

非斉次方程式(3-4)の一つの解（特解）は電源に依存して決まる。しかし、初期値とは無関係である。したがって、これは回路にスイッチを入れて長い間放っておいた状態を表す解（定常状態の解）となっていると考えられる。

コンデンサの充電問題の解

(1) t>0のとき(3-3)の特解はv(t)=Vである。

(2) 式(3-3)の斉次方程式は

(3-9)

となる。その一般解はv(t)=Aexp(-t/RC)で与えられる。

(3) t>0のとき(3-3)の一般解は

v(t)=V+Aexp(-t/RC) (3-10)

となる。t=0でv(t)=0であるとすると、A=-Vとなることがわかる。よって、 t>0のとき(3-3)の一般解は

v(t)=V(1-exp(-t/RC)） (3-11)

となることがわかる。

Spiceでの解析

図3-3に対してSpiceで解析を行う。

　図3-3 RC直列回路

ネットリスト（ C:\SpiceOpus\ex\ex3-1.cir ）は

witch Closing in RC-series circuit
V 1 0 PWL(0,0 10us,1V 10ms,1V)
R 1 2 10k
C 2 0 0.1uF
.TRAN 1ms 10ms
.PROBE
.END

であるとする。

SpiceOpus (c) 1-> C:\SpiceOpus\ex\ex3-1.cir
Circuit: Switch Closing in RC-series circuit

SpiceOpus (c) 2-> run

SpiceOpus (c) 3-> plot v(2)

得られた図(v(t)の変化) (pdf)

3.2　時定数

以上の解析からわかるように、RCという量が、過渡現象がどれくらい続くかを表す量となる。これを時定数という。

3.3　正弦波交流を印加した場合の定常解と過渡解

図3-5のRLC直列回路

回路には時間的にV(t)と変化する電圧源が接続されているとする。

　図3-5 直列RLC回路

回路方程式は

　(3-12)

となる。これは微分積分方程式であまり見かけない形であるが、両辺をtについて微分すると

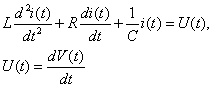　(3-13)

を得る。これは、線形な非斉次（右辺に強制項があるということ）の定数係数２階常微分方程式である。もし、U(t)=0であるなら(3-13)は

　(3-14)

となる。これは線形な斉次（右辺に強制項がないということ）の定数係数２階常微分方程式である。

２階の方程式の解

つぎの方程式の解を求めよう：

　(3-15)

(a) 斉次方程式の一般解

(3-15)の右辺のf(t)をゼロとした斉次方程式を考える。

　(3-16)

(3-16)の一般解を求めるために

(3-17)

の形の解を捜そう。(3-17)を(3-16)に代入すると

(3-18)

を得る。したがって、

(3-19)

が解となる。これより、式(3-16)の一般解は

　(3-20)

となることがわかる。

(a-1) λが小さい場合 ((3-19)のルート中が負となる場合）

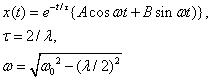(3-21)

となる。これは減衰振動である。

(b)　非斉次方定式の特解

f(t)=F cosωt (3-22)

の場合について(3-15)の特解を求めよう。

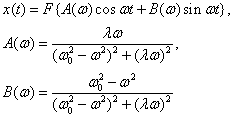　(3-23)

となる。

(ｃ) 非斉次方程式の一般解

非斉次方程式(3-15)の一般解は

　　　非斉次方程式(3-15)の一般解　＝　斉次方程式(3-16)の一般解　＋　非斉次方程式(3-15)の一つの解（特解）

という形をしている。

(d) 解の物理的解釈

斉次方程式(3-16)の一般解(3-20)は斉次であるように、電源によらない。また、A,Bという定数は初期値によって決めるので、初期値に依存する。これは、回路にスイッチが入ったときに、初期条件から定常状態に移行する過程に現れるもの（過渡状態を表す解）である。

非斉次方程式(3-15)の一つの解（特解）は電源に依存して決まる。しかし、初期値とは無関係である。したがって、これは回路にスイッチを入れて長い間放っておいた状態を表す解（定常状態の解）となっていると考えられる。

レポート

1. (コンデンサの放電問題）　図3-1の回路において、t=0でスイッチを2から1へ入れたときの、コンデンサの端子電圧v(t)のt > 0での振る舞いを調べよう。ただし、v(0)=Vとする。

　(1) t > 0でのv(t)の形を解析的に求めよ。

　(2) V=1[V], R=10(1+学籍番号の下３桁/100)k[Ω], C=0.1 μ[F]であるとして、その解の形をscilabあるいはMATLABによりプロットせよ。

　(3) 2の素子値のとき、この問題をSpiceを用いて数値計算せよ。

第３章 回路の定常状態と過渡現象

3.1 コンデンサの充放電