情報系の物理学　演習７

仲沢　由香里

出題日　2000.12.6

提出期限　2001.1.10

提出日　2001.1.10

<問題>

　量子コンピュータによる計算を適当な例をもとに説明せよ。

<解答>

2変数関数を計算する量子コンピュータを考える。

論理関数

すなわち

　　

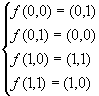
を計算する量子コンピュータは状態空間上のユニタリ作用素

　

で与えられ

が成り立つ。

この命題について、考えてみることにする。

量子コンピュータの定義より、Uはユニタリ作用素でなければならない。つまり、

を満たさなければならない。

よって、条件を満たしていることがわかる。

授業でやったNOTの例より、であるので、

となる。よって、上の命題は成り立つことがわかる。

次に計算結果を得るための観測について考えてみる。

エルミート作用素で表される観測量を使う。

の固有値と固有ベクトルについて考える。

を考えると、

からわかるように、その固有値はである。

に対応する固有ベクトルは

　ただし、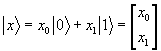

すなわち、成分で書いて、

なる方程式を解くと、となる。したがって、固有ベクトルのノルムが1になるように規格化して

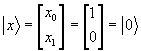
となる。同様にに対応する固有ベクトルは

　となる。よって、の固有ベクトルはそれぞれ固有値0，1に対応している。

同様にして、Iの固有ベクトルはそれぞれ固有値1に対応している。

　　　　ここで、A,BをC²上の作用素とする。Aの固有値とそれに対応する固有ベクトルをそれぞれとし、Bの固有値とそれに対応する固有ベクトルをそれぞれとする。

　　　

　　　が成り立つことから、の固有値とそれに対応する固有ベクトルはそれぞれ

　　　　

　　　で与えられる。

よって、A₁の固有ベクトルは固有値0に対応し、

A₁の固有ベクトルは固有値1に対応することがわかる。

入力がのとき、出力は

であるので、観測の規約より、確率　　で0が観測される。

入力がのとき、出力は

であるので、観測の規約より、確率　　で1が観測される。すなわち、

　　入力がのとき、観測値0が確率1で得られ、

　　入力がのとき、観測値１が確率1で得られる。

したがって、

　　観測値が０ならば、計算結果はであり、

　　観測値が１ならば、計算結果はである。

こうやって、観測値から計算結果を確率１で知ることができる。

次にｆの第２成分を考える。

今度はエルミート作用素で表される観測量を使う。A₁のときと同様に考えると、A₂の固有ベクトル，は固有値０に対応し、A₂の固有ベクトル，は固有値１に対応している。

入力がのとき、出力は

であるので、観測の規約より、確率　　で観測値１が得られる。

入力がのとき、出力は

であるので、観測の規約より、確率　　で観測値０が得られる。すなわち、

　　入力がのとき、観測値１が確率1で得られ、

　　入力がのとき、観測値０が確率1で得られる。

したがって、

観測値が０ならば、計算結果はであり、

　　観測値が１ならば、計算結果はである。

こうやって、観測値から計算結果を確率1で知ることができる。

よって、ユニタリ作用素Uによる状態推移ののちに、観測量A₁とA₂を引き続き観測することによって、論理関数の2つの成分を得ることができ、量子コンピュータによってｆを計算できることがわかった。

<感想>

ユニタリ作用素のことを量子コンピュータというところが面白いと思う。観測という概念も難しいがなかなか興味深いと思った。もう少し、量子コンピュータについて勉強してみたいと思う。

<参考文献>

　上坂吉則著　「量子コンピュータの基礎数理」