忣曬宯偺暔棟妛壽戣儗億乕僩5
採弌擔11寧俀係擔
採弌婜尷侾侾寧俀俋擔
g99p1426忣曬妛壢擇擭
怷拞悞堯
<栤戣>

嵗昗暯柺忋偵丄尨揰O傪拞怱偲偡傞懭墌偑偁傞丅
偙偺懭墌忋偵揰P傪庢傝丄揰P偵偍偗傞愙慄傪峫偊傞.傑偨丄捈慄OP偲懭墌偲偺岎揰偺偆偪丄揰P偱偼側偄曽傪揰G偲偡傞丅傑偨丄懭墌忋偵揰P偲偼柍娭學側揰X傪庢傝丄X傪捠偭偰愙慄偵暯峴側捈慄傪L偲偟丄L偲OP偲偺岎揰傪V偲偡傞丅偙偺偲偒乮PV丒GV乯/乮XV丱俀乯偑X偺偲傝曽偵傛傜偢堦掕偲側傞偙偲傪徹柧偣傛.
<夝摎>
傑偢丄伀偺恾傪尒偰偔偩偝偄.
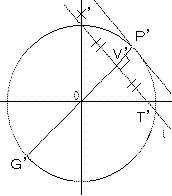
懭墌偺摿庩側応崌偲偟偰墌偺応崌傪峫偊偰傒傞偲.
墌偺応崌偵偟偨偍偐偘偱
鶣乯丂P'V'佦X'V'
鶤乯丂墌廃妏佢X'亖佢G乫
丂
傛傝
仮P'X'V'佷仮T'G'V'
偲側傝丄
曈偺斾
X'V'丗P'V'亖G'V'丗T'V'
X'V'=T'V'傪傆傑偊傞偲丄
P'V'丒G'V'亖T'V'丒X'V'亖X'V'丱俀丂丒丒丒嘇
偙傟傪偦偺傑傑懭墌偵墴偟偮傇偡偲
師偺恾偺傛偆偵側傞.

嶰妏宍偺憡帡娭學偼曵傟傞偑丄曈偺斾偵拝栚偟偰傒傞.
偙傟傜偺係偮偺慄暘偺娭學傪尒傞偨傔偵丄
庢傝弌偟偰尒傗偡偄傛偆偵堏摦偟丄
恾偺傛偆偵妏搙兤,兤',兟,兟'傪婰偡.

懭墌偼墌傪Y幉曽岦傊丂侾/n攞偵墴偟偮傇偟偨傕偺偲偟丄
A亖(1/n)丒{sin兤'/sin兤乸
B亖(1/n)丒{sin兟'/sin兟乸
偲偍偔偲丄
PV亖P'V'丒A
GV亖G'V'丒A
XV亖X'V'丒B
TV亖T'V'丒B
偺娭學偑惉傝棫偮.
偙傟傪嘇偵戙擖偟偰丄曄宍偡傞偲丄
PV丒GV亖(A^2/B^2)丒XV丱俀
亪
PV丒GV亖倠丒XV丱俀
偙傟偼丄懭墌忋偺X傪偳偙偵偲偭偰傕偦傟偵懳墳偡傞墌忋偺X'丄V'丄T'傪峫偊傞偙偲偵傛傝
惉傝棫偮偙偲偑妋偐傔傜傟傞.
<姶憐>
僷儔儊僞兤傪巊偭偰
(x,y)=(acos兤,bsin兤)偲偟偰丄曈偺挿偝偺斾傪弌偡曽朄傕傗偭偰傒偰丄
幚嵺偱偒偨偺偱偡偑丄僌儘僥僗僋側幃曄宍偵側偭偰儗億乕僩偵偡傞偺偼
偪傚偭偲偐偭偙埆偄偺偱丄傛偔巊傢傟傞曽朄偲偟偰丄墌偲偺懳墳娭學傪巊梡
偟偰嶰妏宍偺憡帡偺娭學傪巊偭偰偲偗側偄偐帋偟偰傒偨傜偆傑偔偄偭偨偺偱.
偦偪傜傪弌偟傑偡.
儗億乕僩偺夋憸傪嶌傞帪偵僼儕乕偱庤偵擖傞俵倳倫倎倓傪巊偭偰傒偨傫偱偡偑丄
偄傠偄傠彂偒壛偊傞帪偵柺搢偵側偭偨偺偱巭傔傑偟偨.
庼嬈拞偵丄僼儕乕偺俵倳倫倎倓偼昞帵偑曵傟傞偲峴偭偰偄傑偟偨偑丄僼僅儞僩僒僀僘傪11偵偡傞偲偄偄傒偨偄偱偡.
Mupad僆僗僗儊儁乕僕
http://www.kurims.kyoto-u.ac.jp/~paoon/OriginalDoc/MuPAD.html



