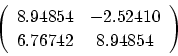シュール分解の計算の命令

Scilabでは複素行列には複素シュール分解を、 実行列には実シュール分解を求めることができる。例題で使い方を示そう。

複素行列   まず、複素行列から始める。

   > A=[i 3;2+i 5];

   > [U S]=schur(A)

   U =

    -0.93426 + 0.06701i  -0.34938 + 0.02437i

     0.31326 + 0.15663i   0.77046 + 0.53267i

   S =

    -0.93485 + 0.42785i  -0.10864 - 1.72261i

     0.00000 + 0.00000i   5.96485 + 0.57215i

となる。Sの対角成分が固有値である。

実行列   次に実行列に対する実シュール分解を求める例を示そう。

   > A=[1 2 3;-5 9 -1;2 6 8];

   > [Q T]=schur(A)

   Q =

    -0.782208  -0.406860  0.471822

    -0.384488   0.911144  0.148274

     0.490225   0.065429  0.869137

   T =

     0.10293   -2.63293  2.39488

     0.00000    8.94854 -2.52410

     0.00000    6.76742  8.94854

シュール分解は相似変換であるから、Tの固有値はAの固有値と一致する。 この場合、Tの固有値は、0.10293と行列

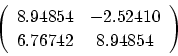$$\left(\begin{array}{cc} 8.94854 & -2.52410 \\ 6.76742 & 8.94854 \\ \end{array} \right)$$ (18)

の固有値となる。