Next: ピボット付きLU分解を求めるコマンド
Up: LU分解法
Previous: LU分解法
Aを
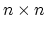 行列、bをn次元ベクトルとするとき、行列方程式
行列、bをn次元ベクトルとするとき、行列方程式
をLU分解法で解くことを考えよう。
行列AのLU分解とは、行列Aを三角行列Lと上三角行列Uの積で
と表すことである。ここで、
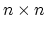 行列Lが下三角行列とは、行列Lの
第i-j成分をLijと書くとき、
行列Lが下三角行列とは、行列Lの
第i-j成分をLijと書くとき、
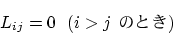 |
(7) |
が成立することである。また、
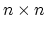 行列Uが上三角行列とは、行列Uの
第i-j成分をUijと書くとき、
行列Uが上三角行列とは、行列Uの
第i-j成分をUijと書くとき、
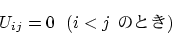 |
(8) |
が成立することである。行列AがLU分解されると
2.5は次のように解かれる。
より、y=Uxと置いて、まず、
を解く。三角行列を係数とする方程式2.10は容易に解くことができる。
実際、
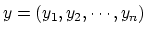 とするとき、2.10を
とするとき、2.10を
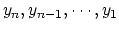 の順に解いていけばよい。この計算はO(n2)回の
浮動小数点数演算でできる。こうして、yが求められたならば、
の順に解いていけばよい。この計算はO(n2)回の
浮動小数点数演算でできる。こうして、yが求められたならば、
を解いて、xを求めればよい。この計算もO(n2)でできる。
s oishi
2000-05-04